Un punto P (ente geometrico) sul piano cartesiano è rappresentato da una coppia ordinata di numeri: le sue coordinate.
Ricorda
Il piano cartesiano è costituito da due rette orientate (o assi) aventi la stessa origine O tra loro perpendicolari. L’asse orizzontale è chiamato asse delle ascisse e l’asse verticale asse delle ordinate.
Fisso un'unità di misura u. Ogni punto del piano è individuato da una coppia ordinata di numeri, le coordinate: il primo numero si chiama ascissa del punto, il secondo si chiama ordinata del punto. Il piano cartesiano si indica con x0y. E' detto cartesiano dal nome del filosofo e matematico francese René Descartes (italianizzato in Cartesio), vissuto nel 1600.
Rappresento (vedi figure 1 e 2) sul piano x0y il punto A di coordinate (3;2). L'ascissa di A è uguale a 3 e la sua ordinata è uguale a 2:
Altri esempi:
Su geogebra puoi rivedere il piano cartesiano:
http://www.geogebra.org/material/simple/id/2653439
Puoi giocare con i punti:
Puoi disegnarli e leggere le coordinate:
LUNGHEZZA DI UN SEGMENTO
Consideriamo due punti di coordinate A(-3;3) e B(4;3) che hanno la stessa ordinata:
Il segmento AB è orizzontale e la sua misura si può determinare contando i quadretti: sono 7, sia che vada da A a B che da B ad A.
La sua misura si può determinare anche calcolando il valore assoluto della differenza fra le ascisse dei due punti:
val. assoluto 4-(-3)=val. assoluto 4+3= 7
val. assoluto -3-4=val. assoluto 4-7= 7
Con segmento parallelo all'asse y i cui estremi sono quelli in figura:
la distanza AB risulta di 5 quadretti, sia che vada da A a B che da B ad A.
Il segmento è verticale e la sua misura si può determinare anche calcolando il valore assoluto della differenza fra le ordinate dei due punti:
val. assoluto 3-(+8)=val. assoluto -5= 5
val. assoluto +8-3=val. assoluto +5= 5
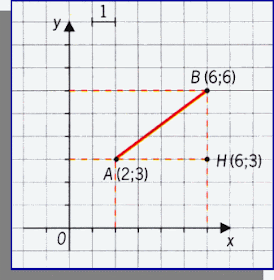
E se il segmento fosse obliquo?
Applicherò Pitagora al triangolo ABH di cui il segmento obliquo è l'ipotenusa.


Applicando Pitagora trovi:

Quindi il segmento è lungo 5.
La formula generale per calcolare la lunghezza di un segmento o, che è lo stesso, la distanza tra due punti, è:

Applicando quanto visto, puoi disegnare e studiare le figure piane calcolandone area e perimetro:



(immagini da brigantaggio.net)
Esercizi
1-Disegna su di un piano cartesiano il poligono avente per vertici i punti A(+3; +2), B(+15; +2), C(+15; +7) e D(+3; +7). Di quale figura si tratta? Descrivi le proprietà della figura ABCD e calcola il suo perimetro e la sua area (poni u=1 cm).
La figura è un rettangolo
2p = 34 cm
A = 60 cm^2
2-In un piano cartesiano rappresenta i punti di coordinate A(-3; -3), B(3; 0), C(1; 4) e D(-5; 1) fissando come unità di misura il centimetro (2 quadretti del foglio corrispondono a 1 cm). Unisci nell’ordine i punti dati e descrivi la figura ottenuta. Calcola la misura del perimetro e l’area del quadrilatero.
La figura è un rettangolo.
2p = 22,36 cm
A = 29,99 cm^2
EQUAZIONE DELLA RETTA
Con geogebra:
Esercizi
Consideriamo due punti di coordinate A(-3;3) e B(4;3) che hanno la stessa ordinata:
Il segmento AB è orizzontale e la sua misura si può determinare contando i quadretti: sono 7, sia che vada da A a B che da B ad A.
La sua misura si può determinare anche calcolando il valore assoluto della differenza fra le ascisse dei due punti:
val. assoluto 4-(-3)=val. assoluto 4+3= 7
val. assoluto -3-4=val. assoluto 4-7= 7
Con segmento parallelo all'asse y i cui estremi sono quelli in figura:
la distanza AB risulta di 5 quadretti, sia che vada da A a B che da B ad A.
Il segmento è verticale e la sua misura si può determinare anche calcolando il valore assoluto della differenza fra le ordinate dei due punti:
val. assoluto 3-(+8)=val. assoluto -5= 5
val. assoluto +8-3=val. assoluto +5= 5
E se il segmento fosse obliquo?
Applicherò Pitagora al triangolo ABH di cui il segmento obliquo è l'ipotenusa.


Applicando Pitagora trovi:

Quindi il segmento è lungo 5.
La formula generale per calcolare la lunghezza di un segmento o, che è lo stesso, la distanza tra due punti, è:

Applicando quanto visto, puoi disegnare e studiare le figure piane calcolandone area e perimetro:



(immagini da brigantaggio.net)
Esercizi
1-Disegna su di un piano cartesiano il poligono avente per vertici i punti A(+3; +2), B(+15; +2), C(+15; +7) e D(+3; +7). Di quale figura si tratta? Descrivi le proprietà della figura ABCD e calcola il suo perimetro e la sua area (poni u=1 cm).
La figura è un rettangolo
2p = 34 cm
A = 60 cm^2
2-In un piano cartesiano rappresenta i punti di coordinate A(-3; -3), B(3; 0), C(1; 4) e D(-5; 1) fissando come unità di misura il centimetro (2 quadretti del foglio corrispondono a 1 cm). Unisci nell’ordine i punti dati e descrivi la figura ottenuta. Calcola la misura del perimetro e l’area del quadrilatero.
La figura è un rettangolo.
2p = 22,36 cm
A = 29,99 cm^2
EQUAZIONE DELLA RETTA
Con geogebra:
Esercizi





Nessun commento:
Posta un commento