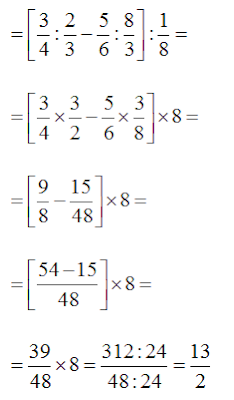Visualizzazione post con etichetta frazioni. Mostra tutti i post
Visualizzazione post con etichetta frazioni. Mostra tutti i post
martedì 16 ottobre 2018
2A- Esercizi di ripasso
mercoledì 10 ottobre 2018
2A-Ripasso aritmetica
GENERALITA' SULLE FRAZIONI
SCHEDA FRAZIONI
Esercizio di rappresentazione sulla retta:
https://www.geogebra.org/m/AyF5RAFY
Divisione con le frazioni
1/3 è dunque la frazione che moltiplicata per 1/2 mi dà 1/3. E' la frazione che cercavamo.
In generale vale la seguente regola:
SCHEDA FRAZIONI
Esercizio di rappresentazione sulla retta:
https://www.geogebra.org/m/AyF5RAFY
Divisione con le frazioni
Sai già che, dati due numeri interi, dei quali il secondo è diverso da zero, si dice quoziente il numero che moltiplicato per il secondo dà per prodotto il primo.
esempio:
20 : 10 = 2
2 x 10 = 20
La stessa regola si applica alle frazioni: il quoziente di una frazione per un'altra diversa da 0 è la frazione che moltiplicata per la seconda dà come prodotto la prima.
Eseguiamo la seguente divisione:
Ora proviamo a moltiplicare la prima frazione per l'inverso della seconda frazione. La prima frazione è 1/6. La seconda è 1/2. il suo inverso è 2. Calcola cioè 1/6 x 2. Il 6 ed il 2 si semplificano, e ti rimane 1/3.
Adesso moltiplica 1/3 x 1/2:
Adesso moltiplica 1/3 x 1/2:
1/3 è dunque la frazione che moltiplicata per 1/2 mi dà 1/3. E' la frazione che cercavamo.
In generale vale la seguente regola:
per dividere una frazione per un'altra, dobbiamo moltiplicare la prima per l'inversa della seconda.
venerdì 6 ottobre 2017
2A - Le frazioni: operazioni ed espressioni
Chi non ha superato il test d'ingresso deve rivedere la teoria.
Operazioni:
Sommare le frazioni:
Moltiplicare facendo la semplificazione in croce:
Divisione:
Espressioni:
Crediti - alcune immagini sono tratte da "aiutodislessia.net"
giovedì 14 settembre 2017
2A- Ripasso delle operazioni con le frazioni
lunedì 18 gennaio 2016
2A - Problemi, frazioni, quadretti
Un esercizio svolto del tipo di quelli proposti in classe e per compito.
Un rettangolo ha l'area di 810 cm². La base è 2/5 dell'altezza. Qual è la loro misura?
Disegno la figura:

La quadrettatura evidenzia che il rettangolo è fatto da 2x5=10 quadratini congruenti di area pari a 810:10=81 cm^2.
Il lato sarà:
l = √Aquadratino = √81 = 9 cm
La base AB è fatta da 2 di questi lati, l'altezza AD da 5. Dunque:
base=9x2=18 cm
altezza=9x5=45 cm
(esercizio di matematicamedie)
Un rettangolo ha l'area di 810 cm². La base è 2/5 dell'altezza. Qual è la loro misura?
Disegno la figura:

La quadrettatura evidenzia che il rettangolo è fatto da 2x5=10 quadratini congruenti di area pari a 810:10=81 cm^2.
Il lato sarà:
l = √Aquadratino = √81 = 9 cm
La base AB è fatta da 2 di questi lati, l'altezza AD da 5. Dunque:
base=9x2=18 cm
altezza=9x5=45 cm
(esercizio di matematicamedie)
2A - Frazioni e numeri decimali (con videolezioni per il ripasso)
FRAZIONI che hanno come DENOMINATORE 10, 100, 1000, 10000, ... si chiamano FRAZIONI DECIMALI perché hanno come DENOMINATORE 10, 100, 1.000, 10.000, etc. (potenze di 10).
FRAZIONI (ridotte ai minimi termini) che HANNO UN DENOMINATORE DIVERSO DA 10, 100, 1000, etc... si dicono FRAZIONI ORDINARIE.
Alcune frazioni ordinarie possono essere ricondotte a frazioni decimali.
Per esempio:
1/4 è equivalente a 25/100. Basta moltiplicare numeratore e denominatore per 25.
3/8 è equivalente a 375/1000. Basta moltiplicare numeratore e denominatore per 125.
4/5 è equivalente a 8/10. Basta moltiplicare numeratore e denominatore per 2.
12/125 è equivalente a 96/1000. Basta moltiplicare numeratore e denominatore per 8.
7/20 equivalente a 35/100. Basta moltiplicare numeratore e denominatore per 5.
Notiamo che 1/4 ha come denominatore 22; 3/8 ha come denominatore 23; 4/5 ha come denominatore 5; 12/125 ha come denominatore 53; 7/20 ha come denominatore 5x22.
Tutti questi denominatori, scomposti in fattori primi, contengono solo 2, 5 o 2 e 5 insieme, senza altri fattori. Le potenze di 10, scomposte in fattori primi, sono 2x5, 22x52, 23x53 etc.
I denominatori delle frazioni considerate possono così essere opportunamente moltiplicate per potenze di 2 o 5 ottenendo una potenza di 10.
DA FRAZIONE A NUMERO DECIMALE
Ogni frazione decimale può essere trasformata sotto forma di numero decimale DIVIDENDO IL NUMERATORE per il DENOMINATORE.
Consideriamo altri esempi:
7/10=7:10=0,7
27/100=27:100=0,27
153/100=153:100=1,53
3/100=3:100=0,03
1/4=25/100=0,25
3/8 =375/1000=0,375
Una frazione decimale si scrive sotto forma di numero decimale scrivendo il numeratore e separando in esso con la virgola, partendo da destra verso sinistra, tante cifre decimali quanti sono gli zeri del denominatore.
Tutti i numeri decimali ottenuti hanno un numero finito di cifre decimali: si dicono decimali limitati.
DA NUMERO DECIMALE A FRAZIONE
Supponiamo adesso di voler trasformare in frazione decimale il numero 6,35.
Scriveremo una frazione che ha per numeratore il numero senza la virgola:
635
e per denominatore 1 seguito da tanti zeri quante sono le cifre decimali del numero dato:
100
Quindi: 6,35 =635/100=127/50 (la frazione che abbiamo ottenuto è stata semplificata)
Una FRAZIONE ORDINARIA, ridotta ai minimi termini, si può trasformare in un NUMERO PERIODICO SEMPLICE se il suo DENOMINATORE NON CONTIENE né il fattore 2, né il fattore 5.
Una frazione ordinaria, ridotta ai minimi termini, si può trasformare in un NUMERO PERIODICO MISTO se il suo DENOMINATORE CONTIENE il fattore 2 e il fattore 5, o uno solo di essi, insieme ad ALTRI FATTORI.
DA NUMERO DECIMALE ILLIMITATO PERIODICO A FRAZIONE
La frazione generatrice di un numero periodico semplice ha:
- per numeratore la differenza tra il numero senza la virgola e la parte intera del numero;
- per denominatore il numero formato da tanti 9 quante sono le cifre del periodo.
La frazione generatrice di un numero periodico misto ha:
- per numeratore la differenza tra il numero senza la virgola e il numero formato dalla parte intera del numero seguita dall'antiperiodo;
- per denominatore il numero formato da tanti 9 quante sono le cifre del periodo seguiti da tanti zeri quante sono le cifre dell'antiperiodo.

(esempi da Quipo e matematicamedie)
Una videolezione sulle frazioni:
https://www.youtube.com/watch?v=d54IByK6NPo
Una videolezione sulla trasformazione di decimali in frazione:
https://www.youtube.com/watch?v=sFZXVJixT1E
IN SINTESI
Una frazione ridotta ai minimi termini che ha al denominatore una potenza del 10 è una frazione decimale; in caso contrario la frazione si dice ordinaria.
Le frazioni ordinarie possono essere: generatrici di numeri decimali limitati se il denominatore scomposto contiene solamente i fattori primi 2 e 5 o solo 2 o solo 5; generatrici di numeri decimali periodici semplici se il denominatore scomposto in fattori primi non contiene né il fattore 2 né il fattore 5; generatrici di numeri decimali periodici misti se il denominatore scomposto in fattori primi contiene i fattori primi 2 e 5 o solo 2 o solo 5 insieme ad altri fattori.
Se il numero decimale è limitato la frazione generatrice ha per numeratore il numero intero ottenuto sopprimendo in esso la virgola e per denominatore la cifra 1 seguita da tanti zeri quante sono le cifre decimali del numero dato.
Se il numero decimale è periodico semplice la frazione generatrice ha per numeratore la differenza tra il numero senza la virgola e la parte intera del numero, e per denominatore il numero formato da tanti 9 quante sono le cifre del periodo.
Se il numero decimale è periodico misto la frazione generatrice ha per numeratore la differenza tra il numero senza la virgola e il numero formato dalla parte intera del numero seguita dall'antiperiodo, e per denominatore il numero formato da tanti 9 quante sono le cifre del periodo seguiti da tanti zeri quante sono le cifre dell'antiperiodo.
FRAZIONI (ridotte ai minimi termini) che HANNO UN DENOMINATORE DIVERSO DA 10, 100, 1000, etc... si dicono FRAZIONI ORDINARIE.
Alcune frazioni ordinarie possono essere ricondotte a frazioni decimali.
Per esempio:
1/4 è equivalente a 25/100. Basta moltiplicare numeratore e denominatore per 25.
3/8 è equivalente a 375/1000. Basta moltiplicare numeratore e denominatore per 125.
4/5 è equivalente a 8/10. Basta moltiplicare numeratore e denominatore per 2.
12/125 è equivalente a 96/1000. Basta moltiplicare numeratore e denominatore per 8.
7/20 equivalente a 35/100. Basta moltiplicare numeratore e denominatore per 5.
Notiamo che 1/4 ha come denominatore 22; 3/8 ha come denominatore 23; 4/5 ha come denominatore 5; 12/125 ha come denominatore 53; 7/20 ha come denominatore 5x22.
Tutti questi denominatori, scomposti in fattori primi, contengono solo 2, 5 o 2 e 5 insieme, senza altri fattori. Le potenze di 10, scomposte in fattori primi, sono 2x5, 22x52, 23x53 etc.
I denominatori delle frazioni considerate possono così essere opportunamente moltiplicate per potenze di 2 o 5 ottenendo una potenza di 10.
DA FRAZIONE A NUMERO DECIMALE
Ogni frazione decimale può essere trasformata sotto forma di numero decimale DIVIDENDO IL NUMERATORE per il DENOMINATORE.
Consideriamo altri esempi:
7/10=7:10=0,7
27/100=27:100=0,27
153/100=153:100=1,53
3/100=3:100=0,03
1/4=25/100=0,25
3/8 =375/1000=0,375
Una frazione decimale si scrive sotto forma di numero decimale scrivendo il numeratore e separando in esso con la virgola, partendo da destra verso sinistra, tante cifre decimali quanti sono gli zeri del denominatore.
Tutti i numeri decimali ottenuti hanno un numero finito di cifre decimali: si dicono decimali limitati.
DA NUMERO DECIMALE A FRAZIONE
Supponiamo adesso di voler trasformare in frazione decimale il numero 6,35.
Scriveremo una frazione che ha per numeratore il numero senza la virgola:
635
e per denominatore 1 seguito da tanti zeri quante sono le cifre decimali del numero dato:
100
Quindi: 6,35 =635/100=127/50 (la frazione che abbiamo ottenuto è stata semplificata)
Un numero decimale è uguale alla frazione che ha:
- per NUMERATORE il NUMERO INTERO ottenuto senza la virgola;
- per DENOMINATORE la cifra 1 seguita da TANTI ZERI quante sono le CIFRE DECIMALI del numero dato.
La frazione si dice frazione generatrice.
Considero adesso:
5/6=5:6=0,83333333333... (si ripete la cifra 3, dopo 8)
5/3=5:3=1,66666666666... (si ripete la cifra 6, subito dopo la virgola)
3/11=3:11=0,2727272727... (si ripetono le cifre 2 e 7, subito dopo la virgola)
5/33=5:33=0,1515151515... (si ripetono le cifre 1 e 5, subito dopo la virgola)
I numeri ottenuti dalle queste frazioni non sono dei numeri decimali limitati: essi, si chiamano NUMERI DECIMALI ILLIMITATI o NUMERI DECIMALI PERIODICI.
per esempio, l numero 0,151515... si scrive 0,(15) oppure 0,15 con una sbarretta sopra il 15 e si legge zero virgola quindici periodico.
Nella parte decimale di tali numeri troviamo dunque una o più cifre che si ripetono all'infinito: tale parte prende il nome di PERIODO. Notiamo che per 0,8333333... tra la VIRGOLA e la PRIMA CIFRA DEL PERIODO c'è un numero (8) che non si ripete. Esso prende il nome di ANTIPERIODO.
0,83333333333... si dice decimale illimitato periodico misto; 1,66666666666... si dice decimale illimitato periodico semplice.
Osserva:
I denominatori delle frazioni 5/3 e 3/11 non contengono come fattori il 2 e il 5.
Il denominatore della frazione 5/6 contiene come fattori il 2 e il 3, cioè il fattore 2 con un fattore diverso da 5.
Il denominatore della frazione 5/33 contiene i fattori 3 e 11 (assenti il 2 e il 5).
- per NUMERATORE il NUMERO INTERO ottenuto senza la virgola;
- per DENOMINATORE la cifra 1 seguita da TANTI ZERI quante sono le CIFRE DECIMALI del numero dato.
La frazione si dice frazione generatrice.
Considero adesso:
5/6=5:6=0,83333333333... (si ripete la cifra 3, dopo 8)
5/3=5:3=1,66666666666... (si ripete la cifra 6, subito dopo la virgola)
3/11=3:11=0,2727272727... (si ripetono le cifre 2 e 7, subito dopo la virgola)
5/33=5:33=0,1515151515... (si ripetono le cifre 1 e 5, subito dopo la virgola)
I numeri ottenuti dalle queste frazioni non sono dei numeri decimali limitati: essi, si chiamano NUMERI DECIMALI ILLIMITATI o NUMERI DECIMALI PERIODICI.
per esempio, l numero 0,151515... si scrive 0,(15) oppure 0,15 con una sbarretta sopra il 15 e si legge zero virgola quindici periodico.
Nella parte decimale di tali numeri troviamo dunque una o più cifre che si ripetono all'infinito: tale parte prende il nome di PERIODO. Notiamo che per 0,8333333... tra la VIRGOLA e la PRIMA CIFRA DEL PERIODO c'è un numero (8) che non si ripete. Esso prende il nome di ANTIPERIODO.
0,83333333333... si dice decimale illimitato periodico misto; 1,66666666666... si dice decimale illimitato periodico semplice.
Osserva:
I denominatori delle frazioni 5/3 e 3/11 non contengono come fattori il 2 e il 5.
Il denominatore della frazione 5/6 contiene come fattori il 2 e il 3, cioè il fattore 2 con un fattore diverso da 5.
Il denominatore della frazione 5/33 contiene i fattori 3 e 11 (assenti il 2 e il 5).
Una FRAZIONE ORDINARIA, ridotta ai minimi termini, si può trasformare in un NUMERO PERIODICO SEMPLICE se il suo DENOMINATORE NON CONTIENE né il fattore 2, né il fattore 5.
Una frazione ordinaria, ridotta ai minimi termini, si può trasformare in un NUMERO PERIODICO MISTO se il suo DENOMINATORE CONTIENE il fattore 2 e il fattore 5, o uno solo di essi, insieme ad ALTRI FATTORI.
DA NUMERO DECIMALE ILLIMITATO PERIODICO A FRAZIONE
La frazione generatrice di un numero periodico semplice ha:
- per numeratore la differenza tra il numero senza la virgola e la parte intera del numero;
- per denominatore il numero formato da tanti 9 quante sono le cifre del periodo.
- per numeratore la differenza tra il numero senza la virgola e il numero formato dalla parte intera del numero seguita dall'antiperiodo;
- per denominatore il numero formato da tanti 9 quante sono le cifre del periodo seguiti da tanti zeri quante sono le cifre dell'antiperiodo.

(esempi da Quipo e matematicamedie)
Una videolezione sulle frazioni:
https://www.youtube.com/watch?v=d54IByK6NPo
Una videolezione sulla trasformazione di decimali in frazione:
https://www.youtube.com/watch?v=sFZXVJixT1E
IN SINTESI
Una frazione ridotta ai minimi termini che ha al denominatore una potenza del 10 è una frazione decimale; in caso contrario la frazione si dice ordinaria.
Le frazioni ordinarie possono essere: generatrici di numeri decimali limitati se il denominatore scomposto contiene solamente i fattori primi 2 e 5 o solo 2 o solo 5; generatrici di numeri decimali periodici semplici se il denominatore scomposto in fattori primi non contiene né il fattore 2 né il fattore 5; generatrici di numeri decimali periodici misti se il denominatore scomposto in fattori primi contiene i fattori primi 2 e 5 o solo 2 o solo 5 insieme ad altri fattori.
Se il numero decimale è limitato la frazione generatrice ha per numeratore il numero intero ottenuto sopprimendo in esso la virgola e per denominatore la cifra 1 seguita da tanti zeri quante sono le cifre decimali del numero dato.
Se il numero decimale è periodico semplice la frazione generatrice ha per numeratore la differenza tra il numero senza la virgola e la parte intera del numero, e per denominatore il numero formato da tanti 9 quante sono le cifre del periodo.
Se il numero decimale è periodico misto la frazione generatrice ha per numeratore la differenza tra il numero senza la virgola e il numero formato dalla parte intera del numero seguita dall'antiperiodo, e per denominatore il numero formato da tanti 9 quante sono le cifre del periodo seguiti da tanti zeri quante sono le cifre dell'antiperiodo.
Etichette:
frazioni,
frazioni generatrici,
numeri decimali
martedì 13 ottobre 2015
2A - Frazioni
Un file con definizioni e procedure:
https://drive.google.com/file/d/0B5xDBpxt-umXYkw3M1NfUkRSZ3c/view?usp=sharing
Problemi
https://drive.google.com/file/d/0B5xDBpxt-umXVE02UnNIaUVGVk0/view?usp=sharing
ESERCIZI
Esercizi interattivi qui (tralascia quelli con l'algoritmo di Euclide).
Frazioni equivalenti - Classe di equivalenza
Osserva l'esempio e completa:
½ = {1/2, 2/4, 3/6, 4/8, 5/10, …}
3/4 = {3/4, 6/8, … , … , …, ... , …}
7/4 = { … , … , … , … , …, ... }
Rispondi:
• 5/7 e 25/35 sono equivalenti? Perché?
• 6/18 e 3/6 sono equivalenti? Perché?
• 7/4 e 14/16 sono equivalenti? Perché?
Addizione
Caso 1- Denominatori uguali
Caso 2 -Denominatori diversi
Trasformo le frazioni date in frazioni equivalenti aventi lo stesso denominatore (il mcm tra 12 e 18, cioè 36):
Ci siamo ricondotti al caso 1: 21/36 + 10/36 = 31/36:
https://drive.google.com/file/d/0B5xDBpxt-umXYkw3M1NfUkRSZ3c/view?usp=sharing
Problemi
https://drive.google.com/file/d/0B5xDBpxt-umXVE02UnNIaUVGVk0/view?usp=sharing
ESERCIZI
Esercizi interattivi qui (tralascia quelli con l'algoritmo di Euclide).
Frazioni equivalenti - Classe di equivalenza
Osserva l'esempio e completa:
½ = {1/2, 2/4, 3/6, 4/8, 5/10, …}
3/4 = {3/4, 6/8, … , … , …, ... , …}
7/4 = { … , … , … , … , …, ... }
Rispondi:
• 5/7 e 25/35 sono equivalenti? Perché?
• 6/18 e 3/6 sono equivalenti? Perché?
• 7/4 e 14/16 sono equivalenti? Perché?
Addizione
Caso 1- Denominatori uguali
 |
| 5/19 |
 |
| 4/19 |
 |
| 5/19 + 4/19 = 9/19 |
 |
| 7/12 |
 |
| 5/18 |
 |
| 21/36 |
 |
| 10/36 |
giovedì 29 gennaio 2015
2A - Frazioni e numeri decimali
Una frazione si dice frazione decimale quando ha per denominatore una potenza di 10.
Altrimenti la frazione si dice ordinaria. Ci sono frazioni riconducibili alla forma decimale.
Per esempio:
½ , che è equivalente a 5/10 (basta moltiplicare per 5 numeratore e denominatore).
7/20, che è equivalente a 35/100 (basta moltiplicare per 5 numeratore e denominatore).
3/25 che è equivalente a 12/100 (basta moltiplicare per 4 numeratore e denominatore).
1/8, che è equivalente a 125/1000 (basta moltiplicare per 125 numeratore e denominatore).
Osserviamo che le frazioni riconducibili a una decimale hanno il denominatore scomponibile nei fattori 2 o 5 o entrambi. Data una frazione ordinaria, dalla scomposizione del denominatore sarà facile vedere se è possibile ricondurla alla forma decimale.
Le potenze di 10 sono infatti:
10=2x5
100=2^2x5^2
1000=2^3x5^3
10000=2^4x5^4 …
La scomposizione è fatta di potenze di 2 e di 5. Moltiplicando i denominatori per le potenze del 2 e del 5 in modo da completare quella del 10 più prossima si trova la frazione equivalente. Guarda gli esempi già riportati.
La frazione 7/20 ha come denominatore 20 che scomposto dà 2^2x5. Basta moltiplicare per 5 per avere 2^2x5^2 cioè 100.
La frazione 1/8 ha come denominatore 8 che scomposto dà 2^3. Basta moltiplicare per 5^3 per avere 2^3x5^3 cioè 1000.
Eseguendo la divisione tra numeratore e denominatore di una qualsiasi frazione ridotta ai minimi termini (non apparente, caso in cui si ottiene un numero naturale) si possono ottenere numeri decimali.
Esempi
35/100=0,35
125/1000=0,125
12/100=0,12
3/10=0,3
Le frazioni decimali danno origine a numeri decimali finiti. Presto incontrerai altri numeri decimali.
Scarica qui la lezione completa.
Altrimenti la frazione si dice ordinaria. Ci sono frazioni riconducibili alla forma decimale.
Per esempio:
½ , che è equivalente a 5/10 (basta moltiplicare per 5 numeratore e denominatore).
7/20, che è equivalente a 35/100 (basta moltiplicare per 5 numeratore e denominatore).
3/25 che è equivalente a 12/100 (basta moltiplicare per 4 numeratore e denominatore).
1/8, che è equivalente a 125/1000 (basta moltiplicare per 125 numeratore e denominatore).
Osserviamo che le frazioni riconducibili a una decimale hanno il denominatore scomponibile nei fattori 2 o 5 o entrambi. Data una frazione ordinaria, dalla scomposizione del denominatore sarà facile vedere se è possibile ricondurla alla forma decimale.
Le potenze di 10 sono infatti:
10=2x5
100=2^2x5^2
1000=2^3x5^3
10000=2^4x5^4 …
La scomposizione è fatta di potenze di 2 e di 5. Moltiplicando i denominatori per le potenze del 2 e del 5 in modo da completare quella del 10 più prossima si trova la frazione equivalente. Guarda gli esempi già riportati.
La frazione 7/20 ha come denominatore 20 che scomposto dà 2^2x5. Basta moltiplicare per 5 per avere 2^2x5^2 cioè 100.
La frazione 1/8 ha come denominatore 8 che scomposto dà 2^3. Basta moltiplicare per 5^3 per avere 2^3x5^3 cioè 1000.
Eseguendo la divisione tra numeratore e denominatore di una qualsiasi frazione ridotta ai minimi termini (non apparente, caso in cui si ottiene un numero naturale) si possono ottenere numeri decimali.
Esempi
35/100=0,35
125/1000=0,125
12/100=0,12
3/10=0,3
Le frazioni decimali danno origine a numeri decimali finiti. Presto incontrerai altri numeri decimali.
Scarica qui la lezione completa.
lunedì 21 gennaio 2013
Frazioni e numeri decimali
Ecco qui, da uno dei nostri siti preferito, una videolezione su frazioni e numeri decimali. Guarda e ripassa la lezione odierna a scuola!
Iscriviti a:
Post (Atom)